テンソルネットワーク学習法で切り拓く量子多体問題の新たな解析手法－複雑な内部自由度を持つ量子系のための新たなアルゴリズム－(大学院理工学研究科石田洋音大学院生、品岡寛准教授)

2025/8/1

プレスリリース全文はこちらからご覧ください。

ポイント

多軌道電子フォノン系におけるファインマンダイアグラムの低ランク構造を世界で初めて発見した。
Tensor Cross Interpolationアルゴリズムを改良しテンソルネットワーク推定の安定性を向上させた。
現実物質のシミュレーションにより、次世代の材料、デバイス開発への応用が期待される。

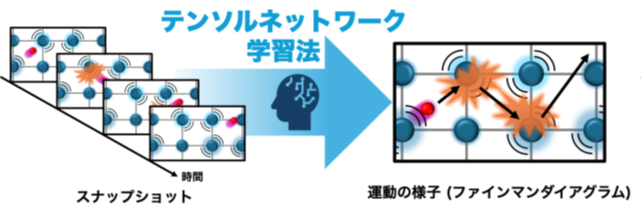
図 1：Tensor Cross Interpolation (TCI, テンソルネットワーク学習法)により、わずかなスナップショットから物質中の電子の運動(ファインマンダイアグラム)を高速かつ高精度に再現。

概要

本研究は埼玉大学大学院理工学研究科の石田洋音大学院生と岡田夏希大学院生(現：千葉大学大学院融合理工学府大学院生)、および同大学の星野晋太郎助教(現：千葉大学大学院理学研究院准教授)、品岡寛准教授との共同研究で実施され、アメリカの国際学術誌『Physical Review Letters』に7月22日付けでオンラインにて掲載されました。

ファインマンダイアグラムは、物質中の電子の振る舞いを記述する基本的な枠組みです。しかし、その数値的評価には多次元積分が含まれ、複雑な系では計算コストが非常に高くなります。これまでは確率的な手法による精度の問題や、計算コスト増大という課題を抱えていました。

本研究では、電子が軌道自由度を持ち、さらにフォノンからの影響も受ける複雑な系を対象に、テンソルネットワーク学習法を適用することで、非常に少ないコストでファインマンダイアグラムを評価できることを発見しました。この方法を用いることで、複雑な電子系に対しても高精度かつ高効率な計算が可能になります。次世代の数値計算手法として、量子物質シミュレーションへの応用が期待されます。

論文情報

掲載誌	アメリカ物理学会　Physical Review Letters
論文名	Low-rank quantics tensor train representations of Feynman diagrams for multiorbital electron-phonon models
著者	石田洋音、岡田夏希、星野晋太郎、品岡寛
DOI	10.1103/tkcp-p5br
URL	https://doi.org/10.1103/tkcp-p5br

用語解説

ファインマンダイアグラム
ファインマンダイアグラムは、電子などの粒子がどのように運動し、他の粒子と影響し合うかを図で表したものです。直線や波線、破線で粒子の動きや相互作用を描き複雑な摂動計算を視覚的に分かりやすく整理できます。物理量を計算するためには、ファインマンダイアグラムが表す多次元積分を数値的に実行する必要があります。

テンソルネットワーク
テンソルネットワークは、大規模なデータを効率的に扱うための数学的な表現方法で、小さなテンソル同士が繋がったネットワーク形式として表されます。多体系の量子力学のように多くの自由度が関係する計算では膨大な情報量が必要であり、そのままでは現代のコンピュータをもってしても計算は困難です。テンソルネットワーク表現を使うことで、重要な部分に着目しながら情報量を圧縮することができ、本質を保ったまま効率的な計算が可能となります。

品岡　寛｜埼玉大学研究者総覧